Determination of the asymptotic limits of adaptive photon counting measurements for coherent-state optical phase estimation

Cover of Determination of the asymptotic limits of adaptive photon counting measurements for coherent-state optical phase estimation

Authors: M. A. Rodríguez-García, M. T. DiMario, P. Barberis-Blostein & F. E. Becerra

Publication: npj Quantum Information

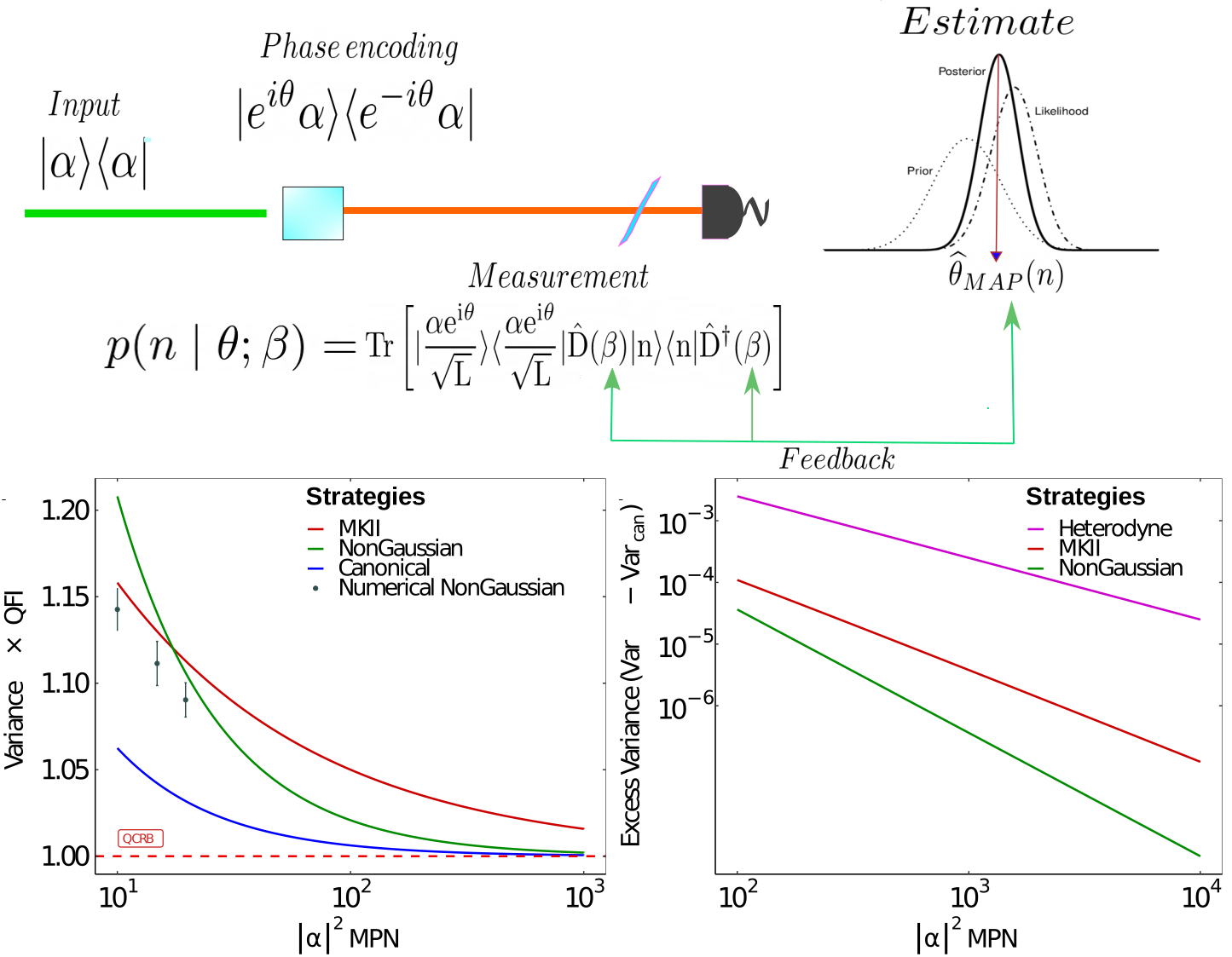
Physical realizations of the canonical phase measurement for the optical phase are unknown. Single-shot phase estimation, which aims to determine the phase of an optical field in a single shot, is critical in quantum information processing and metrology.

Here we present a family of strategies for single-shot phase estimation of coherent states based on adaptive non-Gaussian, photon counting, measurements with coherent displacements that maximize information gain as the measurement progresses, which have higher sensitivities over the best known adaptive Gaussian strategies.

To gain understanding about their fundamental characteristics and demonstrate their superior performance, we develop a comprehensive statistical analysis based on Bayesian optimal design of experiments, which provides a natural description of these non-Gaussian strategies.

This mathematical framework, together with numerical analysis and Monte Carlo methods, allows us to determine the asymptotic limits in sensitivity of strategies based on photon counting designed to maximize information gain, which up to now had been a challenging problem.

Moreover, we show that these non-Gaussian phase estimation strategies have the same functional form as the canonical phase measurement in the asymptotic limit differing only by a scaling factor, thus providing the highest sensitivity among physically-realizable measurements for single-shot phase estimation of coherent states known to date.

This work shines light into the potential of optimized non-Gaussian measurements based on photon counting for optical quantum metrology and phase estimation.

Read the full paper in NPJ Quantum Information at: https://www.nature.com/articles/s41534-022-00601-8 or on the arXiv: https://arxiv.org/abs/2208.06762"

The research is described here.